Alguns dos questionamentos que escutamos com frequência nos treinamentos que a HarboR oferece – seja quando estamos falando especificamente de Controle Estatístico de Processos ou de como usar o InfinityQS para aplicar o CEP – é: E quanto a normalidade? Precisamos de dados normais para poder usar os Gráficos de Controle, certo?
A resposta curta e simples – e que contraria muito do que se diz por aí – é: não, não precisamos de dados normais!
A resposta longa e convincente nós veremos ao longo desse post. Vamos lá?
Porque não precisamos de dados normais
Os Limites de Controle 3sigma são suficientemente robustos para trabalhar com todos os tipos de dados, não apenas com dados normalmente distribuídos. Não é necessário ter dados normais.
A função do Gráfico de Controle é separar a variação de rotina do processo –produzida por causas aleatórias – da variação excepcional – provocada por causas atribuíveis.
O impacto da variação excepcional sobre o processo é, por definição, predominante quando comparado ao impacto das variações aleatórias. Sendo assim, os Limites de Controle precisam filtrar apenas a maior parte da variação de rotina para distinguir o que é ruído do que é sinal do processo. Por isso precisamos de Limites de Controle que cubram toda, ou quase toda variação de rotina.
Para entender como os Limites de Controle 3sigma fazem isso, podemos usar vários modelos de probabilidade para caracterizar a variação de um processo. Na figura abaixo, apresentamos seis modelos – que vão desde a distribuição uniforme até a distribuição exponencial:
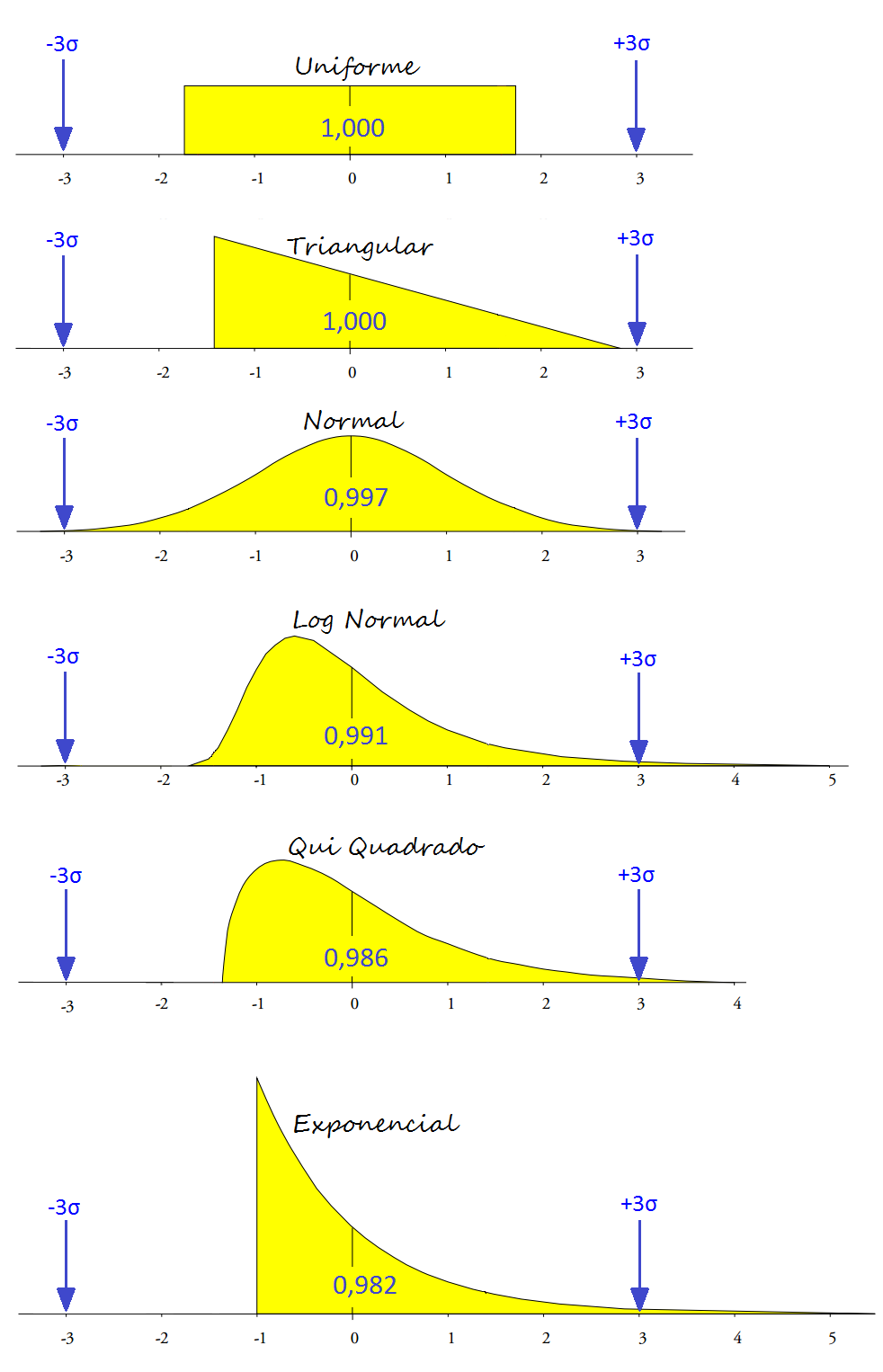No exemplo acima, todos os modelos foram padronizados com média igual a 0 e desvio padrão igual 1. Ao observar os Limites de Controle definidos pela região de -3 a +3 sigma e a proporção da área de cada curva que está dentro desses limites, aprendemos quatro lições:
#1 – Limites de Controle são efetivos para diferente distribuições
O exemplo nos mostra que independentemente do formato da distribuição apresentada pelos processos, os Limites de Controle irão separar praticamente toda a variação de rotina da variação excepcional.
Os modelos de distribuição de dados trabalhados aqui são drasticamente diferentes. Apesar da diferença entre os modelos, os Limites de Controle cobrem de 98 a 100% dos dados.
#2 – Pontos fora dos limites representam sinais
Ao observar as diferentes distribuições estudadas, vemos que qualquer ponto que cair fora dos Limites de Controle é um sinal potencial de uma mudança de processo.
Independente da distribuição que os dados tiverem, é muito pequena a probabilidade de ter um ponto fora dos Limites de Controle e esse dado representar a variação rotineira do processo. É mais provável que qualquer ponto fora desses limites seja um sinal de uma mudança de processo.
#3 – Limites simétricos funcionam para dados assimétricos
Limites de Controle são simétricos por definição, mas funcionam com dados assimétricos. Entre os seis modelos apresentados, quatro são assimétricos.
Não importa o quão assimétricos sejam os dados, o parâmetro de desvio padrão é esticado na mesma proporção que a cauda da curva. Isso significa que o comprimento da cauda alongada determinará efetivamente a distância de três sigma em cada caso. Assim, os limites irão cobrir a maior parte da cauda alongada, não importa o quão assimétricos os dados sejam.
Ter dados assimétricos – ou não ter dados normais – não impede de trabalhar com os Limites de Controle. Porém, é necessário ter nesses casos atenção especial com as regras de alarme ativadas no Gráfico de Controle. É possível que para determinadas regras ocorram alarmes falsos, mas esse é assunto para um próximo post 😉
#4 – Não se preocupe tanto com a incerteza
Qualquer incerteza sobre aonde definimos exatamente os Limites de Controle não afetará consideravelmente a cobertura dos Limites.
Isso porque ao aproximar-se da região de -3 e +3 sigma, independente da normalidade da distribuição, as curvas são tão planas que qualquer erro que possamos cometer ao estimar os limites terão – quando tiverem – um impacto mínimo sobre o funcionamento do Gráfico de Controle.
De onde vêm essas distribuições?
Os seis modelos de probabilidade aqui apresentados são o resumo de um extenso trabalho feito por Donald J. Wheeler – autor de numerosos livros sobre Controle Estatístico de Processos publicados pela SPC Press. Tópicos relacionados a dados normais e os Gráficos de Controle são especialmente trabalhados em seu livro Normality and the Process Behavior Chart, publicado pela mesma editora.
Esses modelos resumem efetivamente o que foi encontrado pelo autor ao examinar 1143 modelos de probabilidade entre 7 famílias de modelos de uso comum. O estudo cobriu 916 modelos em forma de sino, 182 modelos em forma de J e 45 modelos em forma de U. Entre os 1143 modelos analisados, 1112 tiveram mais do que 97,5% da área da curva coberta pelos limites simétricos de 3sigma.
Derrubando o mito dos dados normais
Os Limites de Controle estimados a 3 sigma da média do processo são calculados com base na distribuição normal. Porém, como vimos, isso não significa que os dados precisam ser normalmente distribuídos.
Limites de Controle calculados a três sigma da média são suficientemente robustos para trabalhar com a grande maioria de distribuições de dados. Eles são efetivos para trabalhar com dados descontínuos ou assimétricos, ou seja, quando não temos dados normais.
Por isso:
- Não é necessário nenhum tipo de tratamento de dados antes de colocá-los em um Gráfico de Controle;
- Não é preciso definir uma distribuição de referência antes de estimar os Limites de Controle;
- Também não é necessário transformar os dados antes de colocá-los em um Gráfico de Controle.
Confie na robustez do Gráfico de Controle e lembre-se que quanto mais simples, melhor!
Além do “mito da normalidade”, selecionamos outros 8 erros a evitar na implementação do CEP, continue a leitura!
Se você se interessou pelo conteúdo, conheça mais sobre o Treinamento de CEP que podemos ministrar na sua empresa!
