Por que não usar o desvio padrão global para o cálculo dos Limites de Controle?
Por que não podemos usar o desvio padrão global s – também conhecido como desvio padrão de longo prazo – para calcular os Limites de Controle? Esta é uma dúvida que muitas pessoas têm, principalmente aquelas que estão se familiarizando com os conceitos de Controle Estatístico de Processos (CEP). Inclusive este é um assunto que gera bastante debate nos treinamentos de CEP que a HarboR ministra.
Como já vimos no post sobre o Segundo Fundamento dos Gráficos de Controle de Shewhart, Limites de Controle devem ser calculados com uma estatística de dispersão média¹, que são estatísticas de dispersão dentro do subgrupo (gráfico Xbarra, n>1) ou entre os valores sucessivos (gráfico IX, n=1). Esta estatística é chamada de desvio padrão de curto prazo, geralmente representado pela letra grega σ (sigma).
Relembrando as fórmulas
O desvio padrão de curto prazo σ, é a estatística correta para o cálculo dos Limites de Controle.
Quando trabalhamos com tamanho de amostra igual a 1 (Gráfico de Controle IX-MR), ele é calculado da seguinte forma:
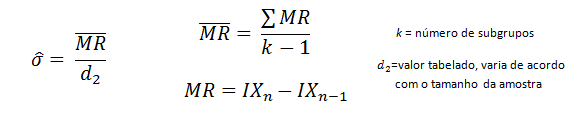
Já o desvio padrão de longo prazo, comumente representado pela letra s, é aquele que aprendemos nas aulas de estatística na faculdade. É calculado da seguinte forma:
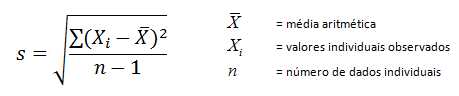
Trata-se de uma medida de dispersão global.
Observe a fórmula: todos os dados são agregados em um único grupo ao mesmo tempo através do cálculo da média aritmética de todos os valores. O uso do desvio padrão global contém a suposição implícita de que o conjunto de dados é homogêneo.
Mas podemos supor que os dados são homogêneos?
Lembre-se que o Gráfico de Controle tem por objetivo separar o que é ruído do processo (variação causada por causas aleatórias), do que é um sinal (variação causada por causas especiais). Ou seja, o objetivo é justamente detectar a ausência de homogeneidade. Por isso, não podemos usar uma medida de dispersão global ao calcular limites para um Gráfico de Controle.²
Exemplo prático
Na tabela abaixo temos dados de 25 medições de diâmetros de uma peça usinada:
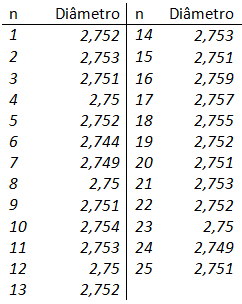
Graficando esses dados, calculamos os Limites de Controle com base no desvio padrão σ (forma correta de calcular) representados pela linha verde pontilhada, e os Limites de Controle baseados no desvio padrão s (forma equivocada de calcular) representados pela linha azul contínua:
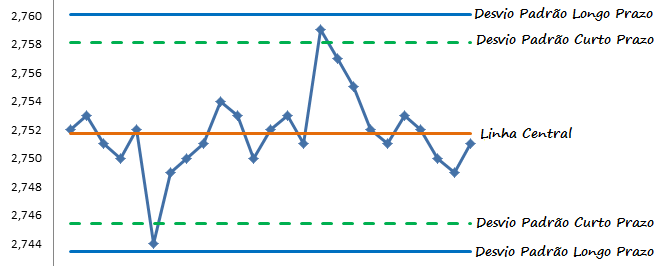
Percebam que os Limites de Controle com desvio padrão de curto prazo σ são capazes de detectar dois sinais de mudança do processo que o limites baseados no desvio padrão de longo prazo s não detectam.
Ou seja, os Limites de Controle σ podem detectar variações especiais que do ponto de vista dos Limites de Controle de desvio padrão s seriam ruídos.
Por que não usar o desvio padrão
Assim concluímos que não se deve utilizar o desvio padrão de longo prazo para o cálculos dos Limites de Controle. Ao aplicar essa medida estatística, você estaria tratando os dados como um conjunto homogêneo, quando na realidade o objetivo do Gráfico de Controle é justamente detectar a ausência de homogeneidade entre os dados.
O desvio padrão σ tende a ser menor pois seu cálculo engloba a variação entre subgrupos subsequentes, com condições mais semelhantes entre si, o que faz com que os Limites de Controle sejam mais justos. O desvio padrão s é calculado com base na distância de cada medição em relação a média global, por isso tende a ser maior, inflando os Limites de Controle.
Assim, utilizar o desvio padrão global no cálculo dos limites de controle pode fazer com que variações especiais – que merecem atenção e deveriam ser investigadas – sejam tratadas como uma variação normal do processo.
(1)Understanding Statistical Process Control – Donald J. Wheeler and David S. Chambers – 2010
(2) Twenty Things you Need to Know – Donald J. Wheeler – 2009

Engenheiro Mecânico pela UFSC, pós graduado em Informática Industrial, fundou a HarboR em 1996. Ao longo desses anos trabalhou com programação, desenvolvimento e implantação de sistemas (MES e CEP), gerenciamento de projetos e equipes. Hoje dedica-se principalmente ao design das soluções e produtos da HarboR, especialmente os voltados para a Indústria 4.0







Opa, vi a pergunta e senti vontade de contribuir. Trabalhei com eng de qualidade em fabricante de pneus e entendo sua dúvida perfeitamente. Resposta à sua pergunta implícita: NÃO PODE TRABALHAR COM LIMITES DE TOLERANCIAS KKKKKKK. Se não alcança 1,33, vc tem de propor um estudo para definir qual valor deve alcançar. Há casos em montadoras em aceitamos 1.0 e até menos e há casos para power train (motor) q exigimos 2.0. No meu caso, qdo eng de qual de pneus a borracha tb tinha variação grande de propriedades e fazíamos utilização de 6 lotes diferentes ao mesmo tempo para obter uma dispersão mediana na entrada da extrusora ou calandra (trabalho pesado no abastecimento das placas de borracha no alimentador ouuuu para o caso de wig wag garantir q estao sendo puxados juntos ao mesmo tempo). O produto q sai das extrusoras geralmente perfilado e calandrado tem variação de detectada no peso/area de produto, certo? na vdd muda a densidade a viscosidade etc, mas controla-se a forma e o peso (controle contínuo a laser ou peso, pra perfil) e peso/area para os calandrados. Meus resultados nunca deram 1,33 para cpk, masssss, a análise de engenharia feita nos resultados, observando dados globais indicavam q não estavámos mal e eram então aprovados com menos, revisão periódica observando tendências. Comparávamos maquinas similares de outras usinas e tb a msm máquina em medições de outros períodos. Mas isso é um “briefing”, trabalhos gigantescos podem ser feitos na cortadeira da extrusao e da calandra para garantir um preenchimento constante do parafuso de extrusão/ massa total acumulada sobre os rolos da calandra (90% por exemplo) pois esse tb tinha variação, qdo menos preenchido o parafuso alterava a pressao na cabeça de extrusao e consequentemente alterava os parametros de controle de peso/ area ou msm na forma do perfil, por exemplo. Trabalhos gigantescos de análise de causas já foram feitos, via DOE (maior parte via teste de frequencias nos equipamentos, testes bem caros hein). Mede se a freqencia de variação de uma propriedade no produto ao msm tempo q mede-se a freqencia gerada pelos equipamentos (por exemplo as rotações por minuto da rosca sem fim por exemplo) e confronta-se para ver se é a causa especial na variação da propriedade do produto ou processo…. anyway, é uma análise difícil, e os resultados devem ser avaliados TÉCNICAMENTE POR ENGENHEIROS/ TÉCNICOS DE PRODUTO e PROCESSO, de acordo com o SPC da AIAG, nem sempre um índice de processo aplicável a um produto aplica-se a outro. Na indústria automotiva, para algumas peças estampadas, em início de produção, adota-se a média da propriedade medida no produto tendente à TS ou TI (conforme o caso), o cp dá bom, mas o cpk nao!, fazendo isso a ferramenta de estampo é feita com as dimensões da tal dimensão próximas ao máx e com o passar do tempo e desgaste do metal da ferramenta de estampagem, a sua média (dimensão medida no produto) vai se aproximando do valor central e obviamente tendendo à outra tolerancia oposta, até ao momento de interromper a venda dessa peça ou fazer uma nova ferramenta. Esse é um caso clássico da eng de produto das montadoras, pois a ferramenta de estampo são eles qem pagam e qerem gastar o mín possível, fazer uma ferramenta q coloque o cpk bom custa no tempo 2 ferramentas. Mas a pergunta q fica é: como o eng de produto libera um cp/pp bom e um cpk/ppk ruim??? avaliação de simulação matemática dos valores de tolerância e via montagem de carro de engenharia onde os gaps entre as peças são medidos, se ficarem inaceitáveis, mudam as especificações, mas geralmente qem manda é o custo da ferramenta q é alto. Entendeu? o índice cp/cpk e pp/ppk é uma referência, e seus valores de aceitação dependem do cliente, no caso das montadoras, por serem IATF 16949, o EQF concede uma derroga dos índices para um valor definido especificamente para aqela commodity, a análise dos dados é para engenheiros e técnicos experientes e deve ser feita, masssss no seu caso aí, vc tem trabalho pra fazer nas máquinas, trabalho q nunca para na vdd, sei bem como é. O parafuso de extrusao qdo desgastado (desgaste heterogeneo nos filetes e zonas de pressao) é obrigado a girar mais, aqece mais, sensibiliza mais a borracha (se a prorpiedade medida for o tempo pra pré vulcanizar…. ferrou, dai só parafuso novo; a cortadeira, geralmente é pneumática… ocorre variação na linha de pressao, se o carregamento é manual ou automatico (no manual os operadores pra poupar trabalho sobre carregam o tapete alimentador etc…. dá pra trabalhar pra alcançar índices melhores sim. Borracha fora dos parametros de perfil, mexe na distribuição de massa no produto final… se for pneu… problema, pré vulcanizada afeta colagem entre camadas e aparecem os grãos… enfim, seu cliente deve ficar sempre reclamando, seu trabalho tem de ser continuoooo. Houve uma ocasião q detectamos via cpk q num dado turno os parametros sempre ficavam piores, e depois de muita investigação descobrimos q umas equipes aceleravam as máquinas para ganhar tempo nas refeições e café e msm assim bater produção, fica esperto kkkkk. abc, sou eng químico, e EQF certificado pela GM, e tb gerente de projetos. A análise dos dados é sempre complexa, varia de área para área da indústria e tb por família de produtos, principalmente qdo um doido de eng de produto fixa um índice q viu na faculdade e depois a gente (EQF) tem de aprovar ou aprovar kkkk (não existe reprovar!), aquele índice num produto sem histórico prévio ao dia do PPAP com produção de 300 peças, mas sempreeeeee, tomo minhas decisões de forma técnica e justificável, e costumo guardar minhas anotações, faço isso presencialmente no processo do fornecedor. Ah e um lembrete, caso seu produto seja pneu: o fabricante entrega os pneus com cpk 1,33 para as montadoras, sempre, blza? E os q não alcançam 1,33 e saem dos limites de controle????? vc deve saber a resposta neh, pro lixo nao vão!!! kkkkk e ainda são vendidos por preço mais alto.
Obrigado pelo artigo.
Voce poderia me ajudar?
Eu trabalho na industria de processamento de borracha, logo, as variações de caracteristicas da minha matéria-prima principal (borracha) é muito ampla. Porem, meus limites de especificação de produto acabado são altos. O que voce sugere, pois é muito dificil trabalhar com cpk de 1,33. E o produto final atende o especificado.
Oi Geison, obrigada por deixar seu comentário.
No artigo falamos sobre limites de controle e não limites de especificação. são coisas diferentes. De uma forma bem resumida: Limite de controle é a “voz do processo” e “Limite de especificação” é a voz do cliente.
Para eu conseguir responder melhor sua dúvida, eu teria que entender com mais detalhes o que você quis dizer no comentário.
Caso tiver interesse, vou deixar meu e-mail por onde podemos conversar melhor, ok? nathalyasalvador@harbor.com.br