O Gráfico de Dispersão, também conhecido como diagrama de correlação, pode ser utilizado para determinar se existe, e qual a intensidade, de correlação entre variáveis. Por isso ele é considerado o passo seguinte ao Diagrama de Ishikawa.
Vamos mostrar um exemplo para facilitar o entendimento:
Utilizamos os dados do IBGE para estudar se existe relação entre a taxa de trabalho infantil e a taxa de escolaridade por faixa de idade entre os anos de 1992 e 2007.
| Taxa escolaridade | ||||||
| Ano | Trabalho Infantil | Média | 5 ou 6 anos | 7 a 14 anos | 7 a 9 anos | 10 a 14 anos |
| 1992 | 23.63 | 78.515 | 53.91 | 86.59 | 87.53 | 86.03 |
| 1993 | 22.73 | 80.9225 | 57.70 | 88.60 | 89.04 | 88.35 |
| 1995 | 21.91 | 83.695 | 63.79 | 90.22 | 90.99 | 89.78 |
| 1996 | 17.57 | 84.44 | 63.77 | 91.26 | 91.76 | 90.97 |
| 1997 | 17.81 | 86.4075 | 66.59 | 92.99 | 93.14 | 92.91 |
| 1998 | 17.06 | 88.3375 | 69.09 | 94.70 | 95.05 | 94.51 |
| 1999 | 16.99 | 89.5675 | 70.96 | 95.69 | 96.22 | 95.40 |
| 2001 | 13.89 | 91.455 | 76.23 | 96.46 | 96.94 | 96.19 |
| 2002 | 13.57 | 92.02 | 77.17 | 96.94 | 97.17 | 96.80 |
| 2003 | 12.61 | 92.5725 | 78.69 | 97.19 | 97.29 | 97.12 |
| 2004 | 12.31 | 93.3875 | 81.83 | 97.19 | 97.61 | 96.92 |
| 2005 | 12.8 | 93.67 | 82.20 | 97.43 | 97.88 | 97.17 |
| 2006 | 11.79 | 94.6875 | 85.29 | 97.73 | 98.37 | 97.36 |
| 2007 | 11.01 | 94.905 | 86.41 | 97.67 | 98.13 | 97.41 |
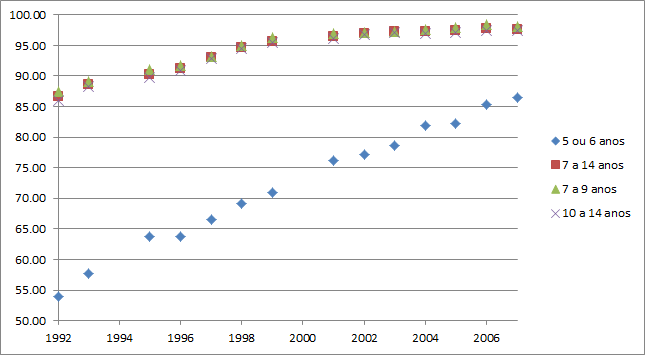
Correlação entre o ano do estudo e a taxa de escolaridade por idade.
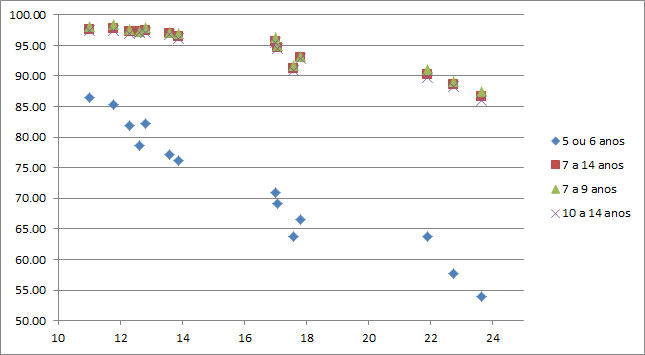
Correlação entre taxa de trabalho infantil e a taxa de escolaridade por idade
Com esses gráficos, podemos concluir que:
- Existe correlação positiva entre o passar dos anos e a taxa de escolaridade. Esta é mais significativa para grupos de crianças entre 5 e 6 anos, ou seja, com o passar dos anos, a taxa de escolaridade por idade aumenta;
- Existe correlação negativa entre a taxa de escolaridade e a de trabalho infantil, ou seja, quanto menor o valor de trabalho infantil, maior o nível de escolaridade das crianças.
A grande vantagem estatística do diagrama de dispersão é relacionar uma variável com outra (x e y) para poder estimar o valor de y com base em x.
Como encontramos correlação nos exemplos apresentados, podemos fazer uma regressão linear e utilizar a equação resultante para prever qual será a taxa de escolaridade para crianças entre 5 e 6 anos no ano de 2010 (dica: temos que tomar cuidado pois a escolaridade máxima é 100. Pode-se ver que a escolaridade para todas as outras idades está praticamente constante a partir de 2001, ou seja, a variação está bem pequena).
Também podemos estimar qual deve ser a taxa de trabalho infantil para alcançarmos escolaridade de 98,00 em crianças com idade entre 10 e 14 anos.
Esperamos que tenha ficado claro o conceito e utilização desta ferramenta da qualidade.
Caso tenha alguma dúvida ou queira discutir outros exemplos, deixe seu comentário aqui embaixo!